Sol LeWitt’s Concepts and Structures
Grade Level: 9–10
Students will consider the term "conceptual art" and the role of math (geometry, fractions, permutations) in producing this art. They will first create a conceptual art piece by following a set of Sol LeWitt’s instructions. Then, they will design two conceptual art plans using math concepts—one in two-dimensions, another in three—for a student-partner to follow.
Sol LeWitt
American, 1928–2007
Four-Sided Pyramid, first installation 1997, fabricated 1999
concrete blocks and mortar, 458.2 x 1012.2 x 970.9 cm (180 3/8 x 398 1/2 x 382 1/4 in.)
National Gallery of Art, Gift of the Donald Fisher Family
Curriculum Connections
- Math (geometry, estimation, fractions, ratio, permutations)
Materials
- Graph paper
- Pencils
- Colored pencils or markers
- Building blocks, sugar cubes, or other geometric polyhedra
- Copies of the “Pyramid Math” worksheet
Warm-Up Questions
Who is the artist when someone comes up with an idea for a work of art but has others make or construct it? Must an artist create a work with his/her own hand to produce a valid work of art?
Backgroud
Sol LeWitt during installation of Wall Drawing No. 681 C at the National Gallery of Art
Photograph by Rob Shelley
National Gallery of Art, Gallery Archives
Solomon LeWitt was born in 1928 in Hartford, Connecticut. His parents were Russian Jews who immigrated to America at the end of the nineteenth century. LeWitt's father, a doctor, died when the artist was six; his mother, a nurse, encouraged his early interest in art. As a young boy, LeWitt took art classes at the Wadsworth Athenaeum in Hartford, Connecticut, where he made art in response to music. He also liked to make drawings on wrapping paper he found at his aunt's shop.
LeWitt majored in art at Syracuse University and was drafted for the Korean War. One of his on-duty jobs was making posters. Some of his first jobs in New York City in the 1950s were graphic designer for Seventeen magazine and for architect I. M. Pei (designer of the East Building of the National Gallery.) He also was a salesman in the bookshop and night receptionist at the Museum of Modern Art.
Sol LeWitt
American, 1928–2007
Wall Drawing No. 681 C / A wall divided vertically into four equal squares separated and bordered by black bands. Within each square, bands in one of four directions, each with color ink washes superimposed., 1993
colored ink washes, 304.8 x 1127.8 cm (120 x 444 in.)
National Gallery of Art, Dorothy and Herbert Vogel Collection
Influenced by his time working in an architect’s office, LeWitt would use assistants to produce three-dimensional works he called "structures." He wrote: "An architect doesn't go off with a shovel and dig his foundation and lay every brick. He's still an artist." Instead of executing the works of art himself, LeWitt comes up with an idea or plan for his art, usually a set of simple instructions—sometimes with line drawings. He then hands over the written plan to his assistants, and they construct the work. LeWitt's instructions are both specific and open-ended so that the resulting work of art varies according to the interpretation made by the draftsperson producing the work of art.
Top:
Set-back skyscraper
Bottom:
Ziggurat Pyramid of Kukulkan, c. 987
Sol LeWitt used lines, geometric solids, ratio, patterns, formulas, and permutations to create his modern structures and wall paintings. The ziggurat and set-back skyscraper had the greatest influence on LeWitt's Four-Sided Pyramid. This structure (LeWitt did not use the term "sculpture" for his three-dimensional art) is made of blocks stacked and stepped back in an orderly pattern and is based on the geometry of the pyramid.
Four-Sided Pyramid is actually made of "double-cubes"—as if two cubes were attached side-by-side. LeWitt became fascinated with the cube and the square in the 1960s. For him, they were "relatively uninteresting . . . and lacked the expressive force of more interesting forms and shapes." Their geometric regularity made them perfect basic components for his art because they could be evenly multiplied, patterned, and permuted into an infinite number of black or white, solid or open structures. LeWitt would come up with a concept or "system" for each structure that described a pattern or sequential relationship for the square or cube. When his plan was complete, he would hand it over—in the form of written notes—to his assistants to build.
Guided Practice
Have students critically analyze LeWitt's Four-Sided Pyramid:
- What do you see? What does this work of art remind you of?
- What do you think this work of art is made of?
- Where would you display this work of art? Why?
- Does this work follow any mathematical principles? What types of math tools—geometry, permutations, etc.—do you think were used? Explain each one.
Sol LeWitt
American, 1928–2007
Floor Structure Black, 1965
painted wood, 47 x 45.7 x 208.3 cm (18 1/2 x 18 x 82 in.)
National Gallery of Art, The Dorothy and Herbert Vogel Collection, Ailsa Mellon Bruce Fund, Patrons' Permanent Fund and Gift of Dorothy and Herbert Vogel
Now have them compare it to LeWitt’s Floor Structure Black:
- Are they both three-dimensional solids? (Floor Structure Black is three-dimensional but unlike Pyramid, it’s open or see-through.)
- Are they monochromatic (one color)? (Yes. During the 1960s, LeWitt used black or white for his structures. Later in his career he started using color.)
- What geometric structure are they based on? (Four-Sided Pyramid looks like neatly-stacked sugar cubes. In fact, LeWitt used blocks that are “double-cubes”—the geometric solid represented by 2/5 of Floor Structure Black. The cube, and its multiples, are key to LeWitt’s conceptual art.)
- How would you describe the pattern? (Repeating.)
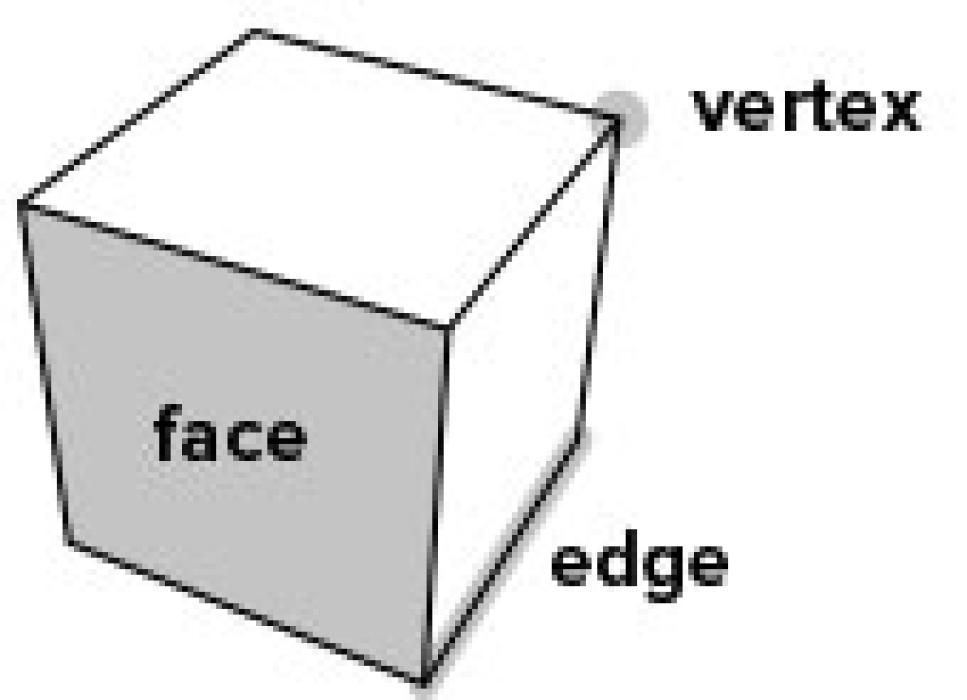
Cubes were "king" for LeWitt's art in the 1960s. What is a cube?:
- How many faces does it have? (6)
- What is the shape of each face? (square)
- How many vertices does it have? (8)
- How many edges does it have? (12)
Now have students calculate the number of blocks in Sol LeWitt's Four-Sided Pyramid by using the “Pyramid Math” worksheet.
Activity
LeWitt used permutation in his conceptual plans to expand his ideas to their limit. In this way, the art would expand objectively. This is how he explained it:
"To work with a plan that is preset is one way of avoiding subjectivity. It also obviates the necessity for designing each work in turn. The plan would design the work. Some plans would require millions of variations, and some a limited number, but both are finite. Other plans imply infinity. In each case, the artist would select the basic form and rules that would govern the solution."
An example of an outcome by following LeWitt’s plan for Wall Drawing No. 26
LeWitt wrote a simple plan for Wall Drawing No. 26. Here it is:
"A one-inch grid covering a 36 inch square. Within each one-inch square, there is a line in one of the four directions."
His instructions are both prescriptive and open-ended, leaving the draftsmen to "play" with arranging the lines within the grid.
Have students experiment with these instructions:
- Using graph paper, students will use colored pencils or markers following the instructions.
- Then students will compare their "LeWitt wall drawing" with their classmates.
- They should discuss how they followed or deviated from the original conceptual art plan, and express any surprises about the completed work: Did it come out as they expected? How would they rewrite the plan?
- Consider this: Who gets the artist credit for this wall drawing, LeWitt or his assistants?
Next, students will come up with their own plan using 2-dimensional geometric figures (lines and shapes) that can be executed on graph paper:
- Students will write a simple conceptual art plan, with no more than 3 instructions.
- They will exchange plans with a partner.
- Using graph paper and a pencil, students will draw each other’s plan.
- Now, they will compare their original plan with the conceptual work of art their partner produced using it.
- Are they surprised with the resulting work? pleased? unhappy with it? How would they rewrite the plan to change the artistic outcome?
- With their partner, they will present their instructions and the resulting works of art to the class.
Extension
Inspired by the cubic structures of Sol LeWitt, students will work with a partner to build various three-dimensional models using building blocks, sugar cubes, or other math manipulatives:
- Have students build a pyramid with a base of 9 cubes, a second floor of 7 cubes, and a third floor of 5 cubes, following this pattern until their structure is complete. Then, ask students: How many cubes high is your skyscraper? (5 cubes high) How many cubes are in it? (25 total cubes)
- Then challenge them to build four different four-sided pyramids with:
- a height of 2 cubes and a base of 4 cubes
- a height of 3 cubes and a base of 9 cubes
- a height of 5 cubes and a base of 25 cubes
- a height of 7 cubes and a base of 49 cubes
- Ask students: How many cubes in each pyramid? (a: 5, b:14, c:55, d:140)
- Students will now write a conceptual art plan with no more than 3 instructions, but this time using three-dimensional concepts. Again, they should exchange with a partner for the other to complete their construction and compare it to their original instructions.
National Core Arts Standards
VA:Cr2.1.HSI Explain how traditional and non-traditional materials may impact human health and the environment and demonstrate safe handling of materials, tools, and equipment.
VA:Re8.1.HSI Interpret an artwork or collection of works, supported by relevant and sufficient evidence found in the work and its various contexts.
